Как понять вероятность?

Вероятность наступления определенного события не всегда соответствует тому, что кажется на первый взгляд. Какова вероятность того или иного результата? Как понимание вероятности может помочь нам повысить прибыль от ставок?

Определение вероятности — это неотъемлемая часть успешного беттинга. Тот, кто не согласится с этим, скорее всего, проиграет в долгосрочной перспективе. Для того чтобы определить вероятность того или иного события, нам необходимо иметь четкое представление о вероятности его наступления — и нам необходимо понимать, какую вероятность предполагают букмекеры для того же исхода и не ошибаются ли они в этой оценке.

Однако здесь есть небольшая проблема. Человеческий разум обладает способностью обманывать нас в определенных ситуациях, и это также происходит с вероятностями. Довольно часто.

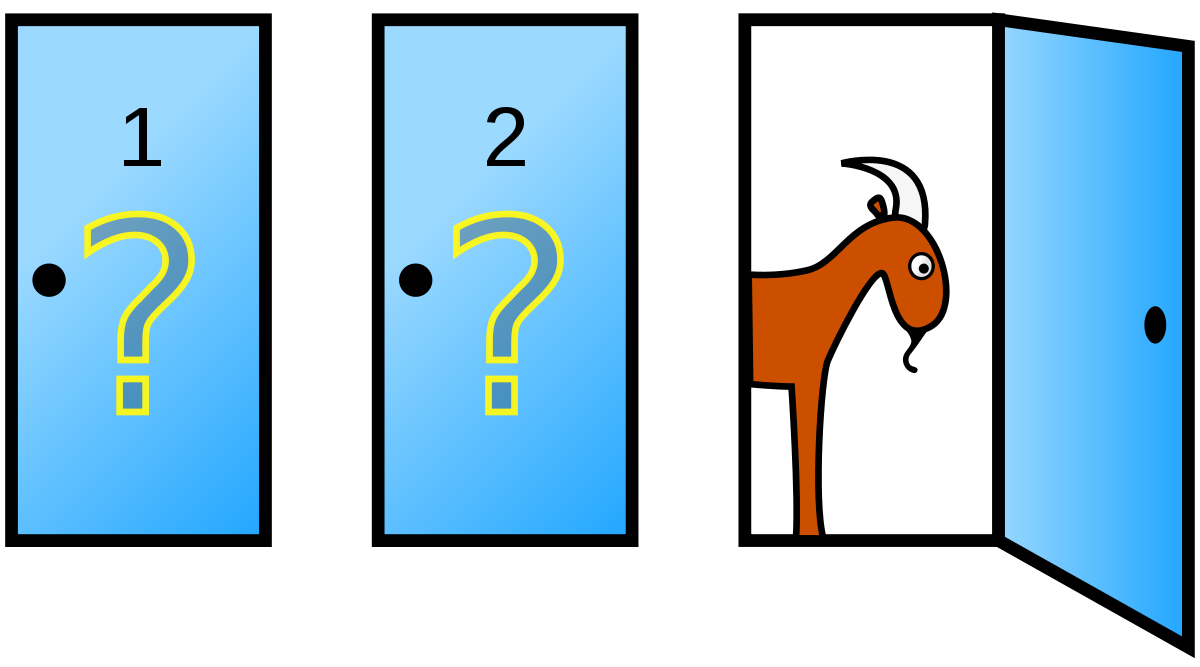
ПРОБЛЕМА МОНТИ ХОЛЛА

Известный пример — так называемая проблема Монти Холла. Рассмотрим следующий сценарий:

Непредвзятый ведущий игрового шоу поставил машину за одной из трех дверей. За каждой из остальных дверей стоит коза. У вас нет никаких предварительных знаний, позволяющих вам различать двери. Сначала вы указываете на дверь, — говорит он. Затем я открою одну из других дверей и там будет коза. После того как я покажу вам козла, вам предстоит сделать окончательный выбор: остаться с вашим первоначальным выбором двери или перейти к другой двери. Вы выиграете то, что находится за дверью». Вы выбираете дверь номер 1. Ведущий показывает вам, что за дверью №3 находится машина.

Теперь вопрос. Как вы думаете, увеличивается ли вероятность правильного выбора двери при выборе второй двери, или она останется неизменной, даже если вы придерживаетесь своего первоначального выбора первой двери? Интуитивно большинство из нас склонны считать, что не имеет значения, будем мы менять дверь или нет — мы предполагаем, что вероятность равна 50% для обоих вариантов. Но, как выясняется, если вы не сделаете выбор в пользу смены, ваша вероятность на самом деле составит всего 33,3%. Соответственно, если вы будете менять варианты каждый раз, ваша вероятность окажется поразительной — 66,7%, или два раза из трех.

Это шутка, да?

На самом деле, нет. Существует множество способов представить возможные исходы для этого сценария, и на самом деле в Википедии есть отличная статья о проблеме Монти Холла, в которой подробно обсуждаются все возможные варианты решений. Но наиболее простым способом представления является следующая таблица, которая охватывает все возможные варианты проведения этого эксперимента. В этой конкретной таблице предполагается, что вы всегда выбираете дверь 1 — но очевидно, что это применимо и к любой другой двери.

Ок, но как так?

Критически важным для понимания этой проблемы является то, что телеведущий не всегда обладает достаточной свободой выбора (поскольку он не должен раскрывать тайну расположения козы). Если за первой выбранной вами дверью находится коза (что происходит в двух случаях из трех), у телеведущего есть только один козел, которого он может показать вам. Таким образом, если вы смените дверь, то окажетесь правы в 66,7% случаев. По сути, телеведущий предлагает вам дополнительную информацию. Если вы решите проигнорировать эту информацию и не поменяете дверь, вы будете правы в 66,7% случаев.

ПАРАДОКС ДНЯ РОЖДЕНИЯ

Парадокс дня рождения — еще один прекрасный пример того, что мы склонны иногда значительно ошибаться в оценке вероятностей. Парадокс дня рождения, как его еще называют, относится к вероятности того, что у любого из людей в определенной группе день рождения приходится на один и тот же день. Как вы думаете, насколько большой должна быть эта группа, чтобы вероятность достигла 50% и 99% соответственно?

Правильные ответы столь же удивительны, как и в задаче Монти Холла: Чтобы вероятность того, что хотя бы два человека в данной группе (ни один из них не близнец) имеют день рождения в один и тот же день, достигла 50%, достаточно, чтобы в группе было 23 человека. Чтобы вероятность достигла 99%, достаточно 57 человек. Поговорим о контр-интуиции.

Опять же, почему?

По сути, мы угадываем цифры, которые намного выше, чем фактический результат, потому что мы склонны делать неверные предположения. Очень важно помнить, что мы ищем вероятность того, что у любых двух человек из группы день рождения приходится на один и тот же день. Если мы возьмем одного конкретного человека, с которым должен совпасть день рождения другого члена группы, а в группе 23 человека, то шансы на совпадение дней рождения будут только у 22 человек. Если вы ищете вероятность того, что у любых двух членов группы день рождения приходится на один и тот же день, вам придется рассмотреть 253 пары (23 умножить на 11 пар), что делает фактические вероятности более доступными для понимания. Если вы хотите углубиться в эту тему, то подробная статья в Википедии о задаче дня рождения также превосходна, но требует некоторой статистической подготовки.

БАНДА «HOLE-IN-ONE»

Важно отметить, что неправильная оценка вероятностей не обязательно является проблемой только для игроков — на самом деле она может повлиять на букмекеров в той же степени и привести порой к исключительно выгодным ставкам. Известный исторический пример — банда «Hole-In-One Gang», состоявшая из двух очень хитрых и метких игроков по имени Пол Симмонс и Джон Картер.

Еще в 1991 году они рассчитали вероятность того, что любой игрок в гольф на турнире попадет в лунку с первого раза. Оказалось, что это не так уж маловероятно, как мы все думаем — на самом деле эта вероятность колеблется около отметки 50% (для любого конкретного турнира). Они объехали всю Великобританию, делая столько ставок, сколько могли ( не забывайте, что это доинтернетная эпоха), поскольку букмекеры по всей стране были рады дать им огромные коэффициенты на эту ставку, с коэффициентами от 4,00 до 101,00 в десятичных коэффициентах — короче говоря, исключительная ценность.

Очевидно, что большинство этих букмекеров были слишком ленивы, чтобы провести необходимую статистическую проверку — но также обратите внимание на очевидное сходство с парадоксом дня рождения. Многие букмекеры, очевидно, полагались на свою интуицию при определении коэффициентов — и, как и в случае с проблемой дня рождения, совершили ошибку, спутав вероятность того, что один конкретный игрок пробьет hole-in-one с вероятностью того, что любой игрок на турнире пробьет hole-in-one с первого раза. Вот что бывает, если не заниматься математикой.

Как выяснилось, в трех из четырех случаев «hole-in-one» были забиты, а Симмонс и Картер, очевидно, добились больших успехов — сообщалось, что они заработали не менее полумиллиона фунтов стерлингов прибыли. В 1991 году это были большие деньги.

Вывод

Из всего этого можно извлечь несколько ценных уроков. Во-первых, человеческая интуиция может сыграть с нами жестокую шутку. Но, более того, она не всегда вредит нашим ставкам. Когда мы правильно ведем игру (или делаем ставки), это явление также может помочь нам обыграть букмекера — или того беднягу, который находится на другом конце наших ставок в букмекерской конторе.